MLP一夜被秒?!全新神经网络架构KAN破纪录!!数学定理全面碾压DeepMind
01 KAN为何一夜爆火?!
机器学习范式就要变天啦?!
近日,一种突破性的神经网络架构——KAN(Kolmogorov–Arnold Networks)诞生啦!!
它的设计哲学与传统的**MLP(多层感知机)**有着明显差异,且在使用更少的参数解决数学和物理问题上显示出了更高的精确度。
举个例子,仅用200个参数的KAN就能重现DeepMind利用30万参数的MLP在发现数学定理方面的研究成果。
这种新架构不仅加强了精确度,同时还揭示了未知的数学公式。而这些研究,DeepMind的成果曾被登载在Nature杂志的封面上呢~
在函数逼近、求解偏微分方程,乃至处理凝聚态物理问题的能力上,KAN都展现出比MLP更出色的表现。

在解决大规模模型问题时,KAN能自然避免灾难性遗忘并且轻松融合人类的直觉偏好或特定领域知识。
MIT、加州理工学院、东北大学等组成的研究团队的这项新研究一经发布,立即在整个科技界引发轰动:Yes We KAN!
KAN与MLP在激活函数的配置上存在显著的差异,这也是二者最为直观的区别之一。
传统MLP的激活函数通常位于神经元上,而KAN则创新地将可学习的激活函数直接置于权重之上。

在作者眼中,这一改动看似“简单”,实则蕴含了深刻的变革。
研究团队在MLP的基础上做出了一个微妙而关键的调整:他们把可以学习的激活函数从神经元(即节点)搬到了连接它们的连接点(即边)上!
这一变化初听起来似无道理,然而它与数学领域的”近似理论”紧密相连,含义深远。

实际上,根据Kolmogorov-Arnold展示理论,在两层网络中,拥有可学习激活函数的边而不是节点,确实显示了更大的潜力。
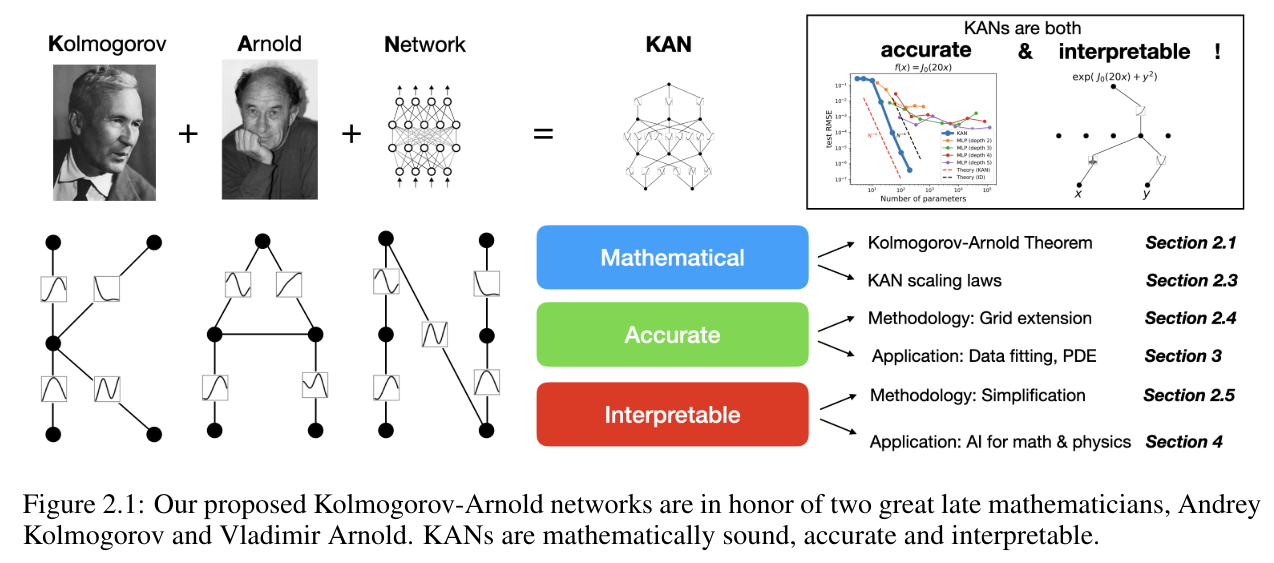
研究人员受到展示定理的鼓舞,将Kolmogorov-Arnold表示在神经网络中明确参数化,具现化了其理念。
而KAN这个名称,也是为了向两位杰出的数学家Andrey Kolmogorov以及Vladimir Arnold致敬,他们的贡献为这一理论提供了基础。
02 KAN如何实现?
2.1 理论根基
柯尔莫哥洛夫-阿诺德表示定理(Kolmogorov–Arnold representation theorem)告诉我们,在有限界限内定义的任何连续的多变量函数,都能够被看做是单变量连续函数的有限叠加。

在机器学习的视角下,这意味着学习高维函数可以转变为学习数量有限的一维函数。
然而,这些一维函数可能在实际应用中是不光滑甚至是具有分形属性的,从而导致在实际中难以进行学习,因此这一定理在机器学习领域曾几乎被认为是不可行的——理论上恰当但实用性弱。
即便如此,研究者们仍然看好该理论在机器学习中的潜力,并且提出如下两项改良措施:
1、而不是局限于原始的方程提到的单一隐藏层(2n+1)以及两层非线性性质,可以将网络扩展为任意的宽度与深度;
2、在科学和日常生活中,多数遇到的函数都较为光滑并含有简单的组合结构,能有利于构造更平滑的柯尔莫哥洛夫-阿诺德表示。这就如同区分物理学家与数学家所关注的焦点:物理学家倾向于探究通常状况下的典型例子,而数学家则更多地考虑极限情况。
2.2 实现细节
KAN网络的设计概念源于通过一系列单变量函数学习多变量函数的简化。
在此框架中,各单变量函数可采用可学习参数的B样条曲线来表示。

研究团队从增加网络层数以加深MLPs的建构概念中获得启示,提出KAN层概念,构成一维函数的矩阵,每个函数均带可学习参数。

依据柯尔莫哥洛夫-阿诺德定理,KAN基层由两类函数组合——内部和外部,对应输入输出维度。
堆叠KAN层增强了深度与表达力,保持解释性,其中每层单变量函数独立学习,易于解读。
此处的f可以看作KAN的具体实现:

03 KAN比MLP强在何处?
在解释性方面,KAN能更好地揭示数据集背后的结构和变量依赖关系,通过符号公式提供洞见。

神经网络缩放效率:与MLP相比,KAN的扩展效率更高。它不仅基于数学的柯尔莫哥洛夫-阿诺德定理,其缩放性能也可通过实验验证得出。

为了证明其有效性,研究团队使用了5个已知可以平滑表达KA(柯尔莫哥洛夫-阿诺德)的案例作为测试数据集,并以每200步增加一个网格点的方式对KANs进行训练,覆盖的G值集合为{3,5,10,20,50,100,200,500,1000}。
将不同尺寸的MLPs作为标准对照,并且在相同条件下,即使用LBFGS优化算法训练1800步,KANs与MLPs的性能通过RMSE(均方根误差)进行比较。
在函数逼近任务上,KAN展现出了比MLP更高的精度

在求解偏微分方程,如泊松方程时,KAN的表现也超越MLP

一个意外的发现是,KAN天生能避免MLP常见的灾难性遗忘问题,为大型模型提供了从根本上避免遗忘的解决方案。

04 小结
关于KAN是否能替代Transformer中的MLP层,社区内部观点分歧。

首先,关键在于学习算法——如SGD、AdamW、Sophia等——是否能为KANs参数找到有效的局部最小值
其次,考虑到在GPU上实施KANs层的效率问题,理想情况下应优于MLPs的执行速度
论文作者还贴心地提供了一个实用的决策树,帮助判断何时采用KAN!

那么,您是否考虑尝试KAN,还是暂时观望?